Optimization of Robot Navigation

June 5, 2016

Demo

Overview

This project was completed jointly with Matt Cruz. The goal was to optimize the navigation of a roomba robot around two circular obstacles to a given destination.

Setup

The iLQR algorithm was primarily used for our optimal control.

At the heart of the control method is a cost function that incorporated quadratic costs imposed on the following:

Where: {x1,y1} = boundary coord., rn= boundary radius, R = input cost coefficient, Q = error cost coefficient, q = state variables {x,y,theta, v1,v2}, qd = desired state variables f(t) (trajectory), tf = final time, C = obstacle cost coefficient.

Therefore the final Cost function for two obstacles was:

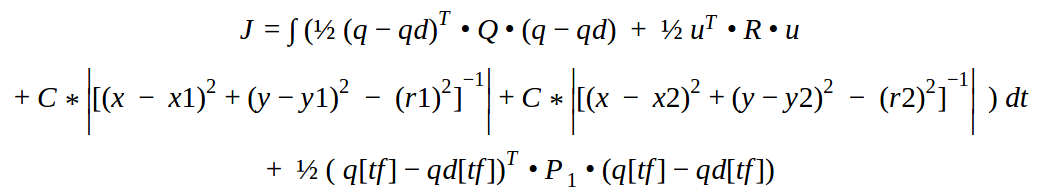
Results

We began our testing with a straight line trajectory ending at the terminal condition. In the middle of this straight line path we placed two circular obstacles. Our intent was to have this straight line curve around the circular obstacles and find its way back to the terminal condition.

During testing we learned two important features, first the weights played a significant role in the performance of the optimizer. Second, we found that we had to re-consider the given initial trajectory.

First Attempt

In our first test we found that a straight trajectory dominated the movement of the roomba. The obstacles were successfully avoided, however the desired trajectory was so highly weighted that the terminal condition we nearly completely ignored. The final path shape thus followed a straight line having trouble breaking from the slope of the desired trajectory, and veering farther and farther away from the end condition.

Tuning

To overcome the influence of the trajectory, avoid the obstacles, and continue on course toward the end point we first adjusted the weighting in the cost function. We increased the weight on P1 to lean more heavily on achieving the end condition and decreased the weight on the deviation from the desired trajectory, Q.

Adjusting Desired Trajectory

We changed the desired trajectory away from a simple straight line (x=t/5, y=t/5) to a motion that was more realistic given our a-priori knowledge of how the roomba needed to “weave” around the obstacles (x=t/5, y=t/5+0.1*sin[t]). By introducing this into the desired trajectory we used the dynamics of the roomba to our advantage.

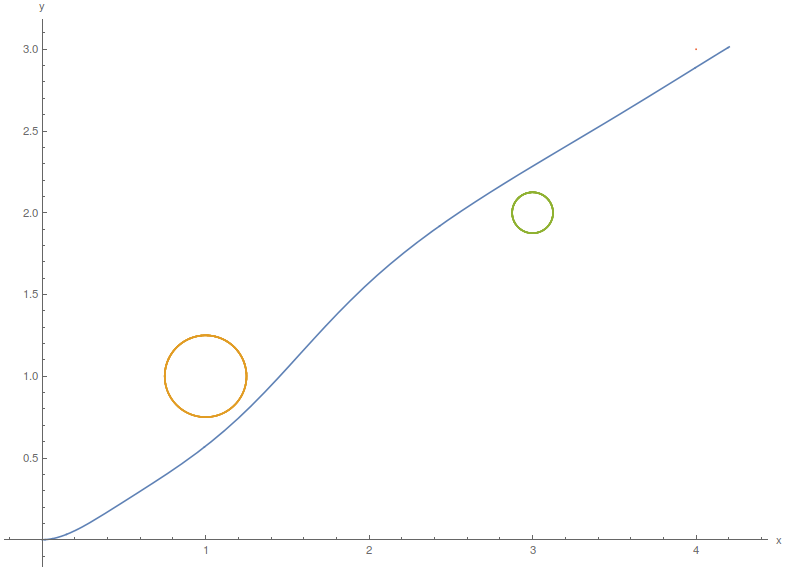
Optimized Trajectory around 2 circular obstacles

Hardware Demonstration

By further tuning the weights on the obstacles, C, and the terminal condition, P1, we achieved a trajectory that narrowly avoided both obstacles and reached the end point. However, running this on the hardware proved incredibly sensitive to the initial conditions. Some adjustment of the hardware setup was needed to recreate the trajectory with the robot.